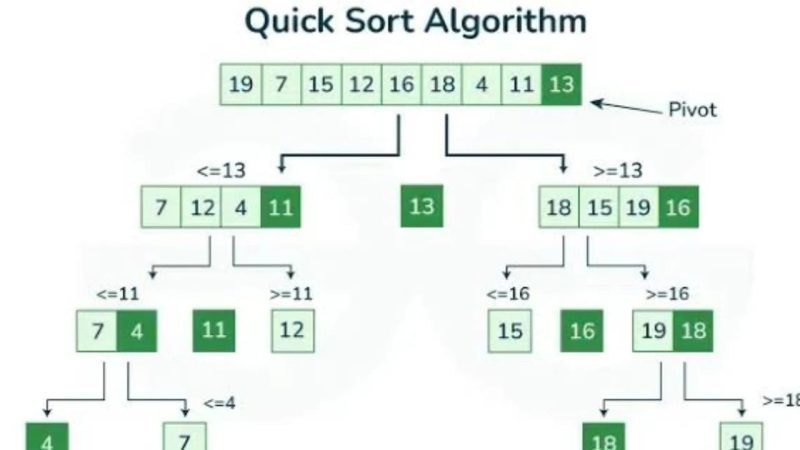
SwaraWarta.co.id – Quicksort adalah salah satu algoritma pengurutan yang paling populer dan efisien, terutama untuk mengurutkan kumpulan data besar.
Algoritma ini dikenal karena kinerja rata-ratanya yang luar biasa, menjadikannya pilihan favorit di berbagai aplikasi ilmu komputer.
ADVERTISEMENT
 .
.SCROLL TO RESUME CONTENT
Kompleksitas Waktu Quicksort
1. Kasus Rata-rata: O(n*log(n))
2. Kasus Terburuk: O(n^2)
3. Kasus Terbaik: O(n*log(n))
Kompleksitas waktu rata-rata Quicksort adalah O(n*log(n)).
Angka ini menunjukkan bahwa Quicksort lebih cepat dibandingkan dengan algoritma pengurutan lain seperti Merge Sort dan Bubble Sort.
Dalam praktiknya, Quicksort sering kali lebih efisien karena operasinya yang dilakukan di tempat dan kurang memerlukan ruang tambahan.
Namun, Quicksort memiliki kompleksitas waktu terburuk O(n^2).
Hal ini terjadi ketika pilihan pivot secara konsisten menghasilkan partisi yang tidak seimbang.
Untuk meminimalisir risiko ini, metode pemilihan pivot acak biasanya digunakan. Pemilihan pivot yang baik sangat penting untuk menjaga kinerja Quicksort tetap optimal.
Kompleksitas Ruang Quicksort
Dalam hal penggunaan ruang, Quicksort juga cukup efisien. Rata-rata, kompleksitas ruang Quicksort adalah O(log(n)).
Ini disebabkan oleh pemanggilan fungsi rekursif dan proses partisi yang dilakukan selama eksekusi algoritma.
Namun, dalam skenario terburuk di mana partisi sangat tidak seimbang, kompleksitas ruang dapat meningkat menjadi O(n). Ini karena tumpukan rekursi yang dalam yang dihasilkan dari partisi yang buruk.
Manfaat Memahami Kompleksitas Quicksort
Memahami kompleksitas waktu dan ruang Quicksort memberikan beberapa keuntungan penting.
Pertama, ini membantu mahasiswa dan profesional dalam memilih algoritma yang tepat untuk tugas pengurutan mereka.
Quicksort menawarkan keseimbangan yang baik antara kecepatan dan penggunaan ruang, terutama dalam kasus rata-rata yang sering terjadi dalam aplikasi dunia nyata.
Kedua, implementasi Quicksort dalam berbagai bahasa pemrograman dapat meningkatkan efisiensi kerja.
Memiliki pemahaman yang mendalam tentang cara kerja Quicksort memungkinkan pengembang untuk mengintegrasikan algoritma ini ke dalam proyek mereka dengan cara yang paling optimal.
Misalnya, mereka dapat memilih metode pemilihan pivot yang paling sesuai dengan karakteristik data yang akan diurutkan.
Ketiga, memahami keterbatasan Quicksort membantu dalam menghindari situasi di mana algoritma ini mungkin tidak menjadi pilihan terbaik.
Dalam kasus di mana ada kemungkinan besar partisi yang sangat tidak seimbang, pengembang mungkin memilih untuk menggunakan algoritma pengurutan lain atau menggabungkan Quicksort dengan teknik lain untuk mengurangi risiko kinerja buruk.
Quicksort adalah algoritma pengurutan yang efisien dengan kompleksitas waktu rata-rata O(n*log(n)) dan kompleksitas ruang O(log(n)) dalam kondisi normal.
Meskipun memiliki potensi kompleksitas waktu terburuk O(n^2), pemilihan pivot yang baik dapat mengurangi risiko ini.
Dengan memahami kompleksitas Quicksort, mahasiswa dan profesional dapat memanfaatkan kekuatan algoritma ini dalam berbagai proyek dan aplikasi, menjadikannya alat yang sangat berharga dalam dunia pemrograman dan ilmu komputer.***